Report of the Pedagogy and Content Issues Subgroup
of the Undergraduate Faculty Program, PCMI, July 1998
Jane M. Day
The pedagogy subgroup of the Undergraduate Faculty Program held three
types of sessions:
- Continuing discussions on the content of linear algebra. This
included discussion of various papers and reviews of selected
textbooks.
- Joint meetings with Math Education Researchers regarding
effective teaching techniques, how students learn, and methods to
assess learning.
- Joint meetings with Math Education Researchers, High School
Faculty and other interested PCMI participants about the TIMMS study
and the new NCTM Standards, and generally to enhance communication
between high school and university level faculty regarding course
content and expectations at each level.
What follows is a summary of the activities of each of these groups.
Section 4 is references and Section 5 contains a list of participants.
Index
- Content of Linear Algebra
Courses
- Effective Teaching Techniques and
Assessment
- Joint sessions with High
School Teachers and Math Educators
- References
- Questions to assess students' deeper
understanding of concepts
- Members of the Pedagogy
Subgroup
1. Content of Linear Algebra Courses
The UFP participants who were most interested in discussing content
and methods formed this Pedagogy Group. First we discussed the
recommendations of the Linear Algebra Curriculum Study Group (LACSG)
and each participant described the content and clientele of the linear
algebra courses they usually teach. We found that the majors, ages
and work experience of the students taking linear algebra varied
dramatically from university to university, as did the level of
abstraction, computer component, type of applications included, etc.
We soon decided it would not be realistic for us to try to update the
LACSG recommendations, as no uniform syllabus would be appropriate for
our courses. But we did agree that anyone teaching linear algebra
should find out what their clientele’s needs are and address those
as best they can.
We decided to focus our time at PCMI on discussing how particular
topics fit into the curriculum, getting better informed about how
students learn, and trying to develop new teaching styles that would
improve students’ learning.
We discussed Carlson's paper [2], in
which he responds to the LACSG recommendatiion for a more matrix
oriented course. He proposes a variety of explorations of properties
of matrices, none of which appeared in linear algebra texts before
1990, but which have since become standard topics. Another
recommendation of the LACSG is that two days be devoted to
determinants. Our participants reported they spend 2-3 days on them,
and that the primary use of determinants in our courses is for
defining the characteristic polynomial and using that to calculate
eigenvalues. Some people also cover Cramer's Rule, and some show how
determinants measure area and volume. We were curious about Sheldon
Axler’s paper "Down with Determinants"
[5], in which he argues forcefully that
they not be taught at all and presents a determinant-free development
of eigenvalue theory. Tom Hagedorn discussed Axler's main ideas and
we agreed that his development is lovely. However for most of our
students, his approach is too abstract, and it is not not a practical
way for students to understand how to calculate eigenvalues. Also,
none of us agreed with Axler that determinants are ugly, useless, and
don’t fit in linear algebra. Our students really like them, and
they are useful in a variety of applications. Equally important,
linear algebra has always had deep connections with combinatorial as
well as continuous mathematics, and determinants are the one topic in
a first linear algebra course where the connection with combinatorial
ideas is apparent.
Dave Morrison led a discussion about articulation – i.e., how well
the linear algebra courses we teach coordinate with the subsequent
courses where linear algebra is needed. We identified a number of
these: multivariable calculus, ODE, physics, scientific computation,
statistics, linear programming, economics, (Lagrange multipliers,
Markov processes), computer graphics, math courses for teachers, and
other math courses such as game theory, graph theory, and coding
theory. We found that only a few of us communicate with the people
who teach such courses, so we really don't know for sure what they
want their students to learn in linear algebra, or whether they are
pleased with what we're teaching. We agreed we need to remedy that,
and that it will probably work best to do that on a one-to-one basis
with faculty in other departments.
Roger Howe and Bill Barker (who were teaching courses for the
undergraduates at PCMI on Lie theory and continuous symmetry) met with
the UFP faculty once, to discuss how topics from representation theory
could be integrated into undergraduate courses. Howe includes
one-parameter matrix groups in his advanced calculus course, and it
seems this would be a lovely topic for a special project in linear
algebra or differential equations. Barker’s continuous symmetry
course is based on a textbook which he and Howe are presently writing,
and this very fresh presentation of geometry would be an attractive
and appropriate upper division course at any college.
2. Effective Teaching Techniques and
Assessment
We had many discussions with Math Education researchers Tim Kelly,
Richard Lehrer, Jeffrey Barrett, Danny Goroff, Mike Battista, Joan
Ferrini-Mundy and Guershon Harel. They talked about how people learn,
and stages of development which a mind goes through as it matures in
its ability to understand abstraction. We discussed the value of
in-depth instruction versus quantity of topics. They suggested ways
technology can improve students’ learning. We did not resolve this
issue, but the message which Harel in particular sends is that it is
pointless for students to study a math topic and not internalize their
understanding of it enough that they can remember and use it later.
It seemed to most of us that he succeeds at Purdue in covering a
remarkable amount in his linear algebra courses, while insisting that
students think through all the theory and mature in their ability to
understand, verbalize and write proofs.
Probably the most important thing these researchers conveyed to us is
that is essential we listen more to our students, to understand how
they are reasoning and where they get stuck. They explained various
techniques we could use: "minute" papers, interview techniques, and
some cooperative learning methods that can increase the interaction of
students with each other and with us. They recommended that we should
develop our "interview" skills: practice asking more
open-ended questions that might reveal how a student is thinking, try
to listen carefully, respect their ideas, and ask more questions when
it appears their understanding is not clear, rather than leaping to
tell them the correct answer. This approach can make class time more
effective. They also suggested we have formal interviews with a few
students occasionally, during office hours, and that we keep notes on
these. They pointed out that most of our students have similar
backgrounds, so even a small number of such interviews could reveal
conceptual difficulties that are common to many students. Jeff
Barrett showed a videotape to help us understand how to conduct such
interviews. Open-ended questions would be ones like "explain what
linear independence means to you" and "how are you thinking about this
problem."
Danny Goroff presented two videotapes [6,7].
The first, "A Private Universe," shows Harvard University
graduates who do not understand the fundamental science fact about why
the earth has seasons. This led to a discussion regarding whether
students know and retain the knowledge we think we are imparting. The
second tape, "Thinking Together, Collaborative Learning in
Science" illustrated effective teaching techniques with a large
lecture class in science using quick questions given to the class,
informal short discussions between students and polling of
answers.
We had two very provocative discussions with Guershon Harel, who
has been teaching linear algebra and doing research on how students
learn the subject for more than ten years. One of the LACSG
recommendations was that geometric interpretation of concepts should
always be included in linear algebra, and most textbooks written since
that time include such interpretations. Discussions about the LACSG
report continue at professional meetings, and one of the things that
many people report is that students seem to understand concepts like
span, independence and subspace much better now than they used to.
(Presentations of linear algebra used to be heavily algebraic.) So
were were somewhat amazed at what Guershon told us. He has become
convinced recently that it is a mistake to motivate such
concepts by first giving examples in R2 and R3.
His research indicates that when he does that, many students are never
able to let go of these visualizations and handle such concepts
effectively in Rn. His work indicates it is better to
first define each concept in Rn, then give examples which
include the geometric visualizations in low dimensions as well as some
other type examples. The point seems to be, "first impressions
are powerful," so we should be careful that students’ first
impression of each concept is reasonably complete. We’re not all
convinced, because geometric motivation can be so powerful. Indeed,
Guershon says that’s the only way he knows how to effectively
introduce the method of least squares approximation. But some of us
will probably try Guershon’s recommendation with some concepts.
We read and discussed a number of articles suggesting ways to teach
linear algebra more effectively
[2,
3,
4,
8,
9,
10,
11]. We also read some
papers from the physics literature about two "concept inventories"
which have been developed by the physics community in the past decade
[12,
13,
14,
15].
These have qualitative rather than quantitative
questions, and their purpose is to evaluate students' real
understanding of force and mechanics after they complete a
calculus-based physics course. Apparently these inventories have
revealed fundamental misconceptions, among large numbers of students,
about Newton's laws -- including many students who had performed well in
very demanding courses. Considerable analysis has been done of
students' answers, and there is much discussion among physics faculty
throughout the country about how to change the way physics is taught,
to improve students’ fundamental understanding.
Our Pedagogy group had not heard before about this work, and found it
intriguing. We talked about trying to develop a similar concept
inventory for linear algebra, and we made some preliminary progress
toward this goal. We divided into four subgroups to think about these
topics: linear systems; inverses; eigenvalues; and subspace, basis and
dimension. Each group was to identify the major concepts in its topic
and develop some questions that would be suitable for assessing
students' deeper understanding of that topic. The reports of these
groups are attached. Some of the questions we developed are more
appropriate for oral interviews, others for a written inventory. We
agreed that developing a concept inventory for linear algebra is a
bigger task than we could accomplish. For one thing, our group may
not be sufficiently representative, and we as individuals need to find
out more about how our students are thinking. So for now, we are
simply going to try using questions like these in interviews and on
tests.
3. Joint sessions with High School Teachers
and Math Educators
Gail Burrill (former president of NCTM) met with us. We were all
surprised to hear that some matrix topics have been in most high
school texts for 7-10 years (if our students know these things, they
have been keeping it quiet!). She also told us that the new NCTM
recommendations for high school mathematics include more linear
algebra topics and applications that use matrices. Curriculum
material has been written to follow the new guidelines, and this is
being used in selected places around the country. This new material
will start appearing in major publishers' books within a year or two.
We asked about teacher training and Gail admitted that there is no
coherent plan to provide that, and this is a problem. We wonder if
master teachers could be identified in schools, who could receive
special training and then teach their colleagues. Some of the high
school teachers at PCMI told us that such training would be quite
attractive if it earned some college credit.
Dan Kalman led a discussion between the High School Teachers,
Undergraduate Faculty and Math Education Researchers. These teachers
were clearly a very dedicated and talented group. They explained what
topics they cover in various courses, especially the geometry and
matrix topics they teach. We talked about how curricula at the
secondary and college levels affect each other, and expressed a
fervent wish that students learned some analytic geometry in
R3 before college. They really need to understand vectors,
lines and planes in R3 in third semester calculus and in
linear algebra. In fact we would much prefer they learn solid geometry
in high school rather than calculus or matrix topics. The high school
teachers admitted that 3-d analytic geometry is not taught any more,
but explained that is because of heavy pressure from parents to
prepare students for the AP calculus exam. Solid geometry is not on
that test so it has been dropped from high school texts. In fact,
matrix topics are not essential for that exam either and tend to get
skipped when time is limited. It was clear that more communication
between high school and college educators could benefit everyone, and
the participants were urged to explore avenues to encourage regular
exchanges.
4. References
The first five references below are from Resources for Teaching Linear
Algebra, ed. D. Carlson, C.R. Johnson, D. Lay, D. Porter, A. Watkins
and W. Watkins, MAA Notes 42, 1997. This is a collection of 28 papers
on many topics related to linear algebra: what clients need; ideas on
what and how to teach, including thoughts on incorporating computer
use; applications; and special topics.
- The Linear Algebra Curriculum Study Group
recommendations for a first course in linear algebra, D. Carlson,
C.R. Johnson, D. Lay and D. Porter.
- Teaching linear algebra: must the fog always
roll in? D. Carlson, 39-58.
- Some thoughts on a first course in linear
algebra at the college level, E. Dubinsky,85-106.
- The Linear Algebra Curriculum Study Group
recommendations: moving beyond concept definition, G. Harel,
107-126.
- Down with determinants! S. Axler, 179-200.
- A private universe, M.H. Schneps, Project Star,
Derek Bok Center, Harvard University.
- Thinking together, collaborative learning in
science, Derek Bok Center, Harvard University.
- Case number one: force and inertia, a case about
teaching introductory physics, G. Goroff and J. Wilkinson. Response
to case number one: hockey pucks, monkeys and misconceptions. These
two papers are in Change (Nov./Dec. 1993), 22-29.
- Viewing some concepts and applications in linear
algebra, T. Hern and C. Long, in Visualization in Teaching and
Learning Mathematics, ed. W. Zimmerman and S. Cunningham, MAA Notes
19, 1991.
- Students' proof schemes: results from exploratory
studies, G. Harel and L. Sowder, CBMS Issues in Education, vol. 7,
1991.
- Two dual assertions: the first on learning and
the second on teaching (or vice versa), G. Harel, American
Mathematical Monthly 105 (1998), 497-507.
- Force concept inventory, D. Hestenes,
M. Wells and G. Swackhamer, Physics Teacher 30 (1992),
141-151.
- A mechanics baseline test, D. Hestenes and
M. Wells, Physics Teacher 30 (1992), 159-
- What does the force concept inventory actually
measure? D. Huffman and P. Heller, Physics Teacher 33 (1995),
138-143.
- Performance on mechanics concept inventory
tests – diagnostics and complementary exam problems, Physics
Teacher 35 (1997), 150-155.
5. Questions to assess students' deeper
understanding of concepts
Eigenvalues and Eigenvectors
These are some questions that are suitable for interviews with
students designed to explore their understanding of eigenvalues and
eigenvectors.
- What motivates the concepts of eigenvalue and eigenvector for
you?
- What is the definition of eigenvalue and eigenvector?
- Given a matrix A, how do you compute the eigenvalues and
eigenvectors?
- Can you give a use of eigenvalues and eigenvectors other than the
one you mentioned in response to question 1? How about another?
- How many different eigenvectors are there associated with a given
eigenvalue?
- Given a matrix A, can you find enough eigenvectors to form a basis?
- What is the difference between the algebraic multiplicity and the
geometric multiplicity of an eigenvalue?
- What is a generalized eigenvector? Why are they important?Suppose a matrix A is symmetric. What is special about its
eigenvalues and eigenvectors?
It is intended that each question would be the start of a
conversation. The follow-up questions would be natural follow-ups to
the student’s responses.
While these questions provide a good starting point, we are reluctant
to claim they form anything close to a finished list. The list was
compiled in too short a time to assure that.
Systems of Linear Equations
- Major concepts.
- Algebraic and geometric descriptions of the possible types of
solution sets
- Algebraic and geometric descriptions of a solution set
- The Superposition Principle – i.e., using solutions of
Ax = 0, Ax = b1 etc. to
construct solutions to other systems.
- Rank
- Least squares solutions
- What we want a student to be able to do:
- Describe a linear system in matrix form if it is given as a set
of equations, and vice versa.
- Explain both algebraically and geometrically why there are only
three basic possibilities for the solution set to a linear system
(empty, or a single point, or an infinite set of points).
- Describe both algebraically and geometrically how the following
two sets are alike and how they differ: the solution set of
Ax = 0 and the solution set of Ax = b
when b ¹
0.
- If A, b1, and b2 are known
and solutions of Ax = b1 and Ax =
b2 are given, write a solution for Ax =
b3 when b3 is in the span of
{b1, b2}.
- Explain both algebraically and geometrically what a "least
squares solution" to a linear system Ax = b means, why
such a solution must always exist, and at least one way to calculate
one.
- Sample questions to determine a student's knowledge. The
first 11 would be appropriate for a written test or interview.
- Consider this system of equations: x – 4y + 7z = 3 and x
– z = -1.
- Write the system of equations above as a matrix equation
Ax = b (that is, define A and b).
- Which one of the following statements is correct?
- The system is inconsistent.
- The solution set for the system is the single point
(-1,-1,0).
- The solution set for the system is all vectors of the form
t(-1,-1,0), where t can be any real number.
- The solution set for the system is all vectors of the form
t(1,2,1) + (-1,-1,0), where t can be any real number.
- None of the above is correct.
- Consider this system of equations: 2x – y + 4z = 2 and x +
y – z = 7. What does the solution set look like
geometrically?
- a single point
- a line
- a plane
- a circle
- none of the preceding
- not enough information
- Suppose A is a 3x3 matrix, y ¹
0 and Ay = 0. Will there be a solution to
Ax = b for every b in R3?
Explain.
- Two planes in R3 can intersect in various ways.
Check the items in the following list that could be correct:
- The planes intersect in a single point.
- The planes intersect in three points.
- The planes intersect in a line.
- The planes do not intersect.
- Suppose you have three linear equations in three variables. Which
of the following could be the solution set for such a system? Check
all that are possible:
- a single point
- the empty set
- a line
- a parabola
- a plane
- a circle
- all of R3
- Suppose A is a 2x2 matrix which has rank one. Which one of the
following describes the solution set to Ax = 0?
- a line
- a single point
- a circle
- all of R2
- none of these
- Let A =
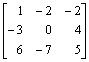 and b =
and b = . Is
. Is 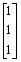 a solution for the system
Ax = b? Explain.
a solution for the system
Ax = b? Explain.
- Suppose A is a matrix and v and w are
solutions to Ax = 0.
- Is 2v also a solution to Ax = 0? Why or
why not?
- Is v + w also a solution to Ax =
0? Why or why not?
- Suppose b¹
0 and Ax =b is consistent. Describe how the
solutions of Ax = b are related to solutions of
Ax = 0.
- Let A be a 2x3 matrix. Suppose that y0 is
a solution to Ax =
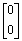 , y1 is a solution to Ax =
, y1 is a solution to Ax =
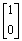 , and
y2 is a solution to Ax =
, and
y2 is a solution to Ax = 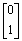 .
.
- Is 3y0 + y1 +
5y2 a solution to Ax =
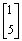 ?
?
- Write a solution to Ax =
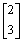 .
.
- Write all solutions to Ax =
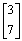 .
.
- Can Ax = b can be solved for every b
in R3? Explain.
- A certain matrix A has reduced echelon form
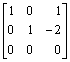 . Find all
solutions to Ax = 0.
. Find all
solutions to Ax = 0.
- A certain matrix A and vector b are such that the
augmented matrix [A b] has reduced echelon form
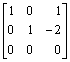 . Find all
solutions to Ax = b.
. Find all
solutions to Ax = b.
The following questions are more appropriate for a verbal interview,
because students learn different methods for solving least squares
problems.
- Suppose A is a 40x3 matrix and b is a 3x1 column
vector. Let W denote the span of the columns of A. Suppose
b is not in W, as indicated in the sketch.
- Explain what a least squares solution for Ax = b
is.
- Explain why a least squares solution must exist for Ax =
b.
- Explain a method for finding a least squares solution for
Ax = b.
- Suppose b is in W, so Ax = b is
consistent, and suppose v is a least squares solution for
Ax = b. Is v a true solution of Ax =
b? Explain.
Invertibility
The core facts about an invertible nxn matrix A:
- There exists B such that AB=BA=I.
- Ax=b has a solution for every column vector b.
- The linear map from Rn into Rn defined by
x à Ax is one-to-one and onto.
- The set of all row vectors (column vectors) of A is a basis for
Rn.
- det(A) is nonzero.
- Algorithm for calculating A-1: [A | I ] ~ [I |
A-1 ].
- If B is another nxn invertible matrix, (BA) -1 =
A-1B-1
Some problems designed to test students' understanding of these basic
concepts:
- By trial and error, some students working with a particular 3 by
3 matrix A discover several solutions to the equation Ax =
[5,8,11]t, including [0,1,0]t and [2,0,0]t
. Then one of students suggests finding the inverse of A as a
more systematic way to find solutions. Do you agree with this
suggestion? Explain why.
- A and B are 4 by 4 matrices, that are inverses of each
other. Which of the statements below are true? There are may be more
than one correct statement. Explain why the ones you select are
correct.
- If Av=w then Bv=w.
- If Av=w then Bw=v.
- If Av=w then Aw=v.
- If Bv=w then Av=w.
- If Bv=w then Aw=v.
- Given a 5 by 5 matrix A and a vector b in R5 , which of
the following are possibilities for the system Ax=b? (More than one
may be possible.)
- The system has no solutions.
- The system has exactly one solution.
- The system has exactly two solutions.
- The system has a very large finite number of solutions.
- The system has an infinite number of solutions.
- Suppose A is a noninvertible square n-matrix and b is a vector in
Rn. Is it possible for the equation Ax=b to have a
solution? Explain briefly your answer.
- Suppose A is an invertible 2 by 2 matrix. Which of the following
statements is true? Explain why.
- Ae1 is invertible, where
e1=[1,0]t.
- Ae2= [0,0]t, where
e2=[0,1]t.
- {Ae1, Ae2} is linearly independent.
- Ae1=Ae2.
Linear Combinations, Linear Independence, Span,
Basis, Dimension, and Subspace
Our Rationale: We felt that the basic problem that students encounter
when seeing these ideas for the first time in a linear algebra course
is their unfamiliarity with how to work with definitions in a
mathematically precise way. The fact that these unfamiliar definitions
are usually encountered one after another in rapid succession---the
definition of a span depends on an understanding of linear
combinations, the definition of a basis depends on the ideas of linear
independence and spanning sets---magnifies this problem.
Consequently, our goal was to develop exercises which tested a
student's understanding of these definitions by asking questions which
required geometrical intuition and working directly with the
definitions.
- Given two vectors v1 and v2 in a coordinate
plane, sketch the set {a1v1 +
a2v2 | 0 < a1,a2 <
2}.
- Suppose we have two vectors in R3 that span a
plane. Are they independent? Consider a third vector. How would you
describe geometrically where to put the third vector so that the
resulting set is a linearly independent set? A linearly dependent
set?
- Given a coordinate plane with vectors v1 and
v2 and points A, B, and C drawn in the plane, estimate the
constants a1 and a2 such that
a1v1 + a2v2 is A, B, or
C, respectively.
- Suppose a set of vectors spans R3. What can you say
about how many vectors are contained in this set? Will every set of
elements of R3 with this number of vectors span
R3?
- Suppose that {v1,...,vn} are linearly
dependent. Must v1 be a linear combination of
v2,...,vn? Explain.
- Suppose v1,v2,v3,v4
are vectors in R2 which span R2. Do
v1 and v2 span R2?
- Suppose {v1,v2},
{v1,v3}, and {v2,v3} are
linearly independent sets. Must the set
{v1,v2,v3} be linearly
independent?
- Two nonzero vectors are independent if and only if the angle
between them is neither 0o nor 180o. Can you
find conditions on the angles between three nonzero vectors that would
tell you whether or not they form an independent set?
- Is R2 a subspace of R3? Explain.
6. Members of the Pedagogy Subgroup
Daniel Goroff
Department of Mathematics
Harvard University
Science Center 325
Cambridge, MA 02138-2901
goroff@abel.math.harvard.edu
Fernanda Botelho
University of Memphis/Institute for Mathematics
514 Vincent Hall
206 Church St. SE
Minneapolis, MN 55455
botelho@irna.umn.edu
Harold Davenport
Department of CS, Mathematics and Statistics
Mesa State College
Grand Junction, CO 81502
davenpor@mesa5.mesa.colorado.edu
Jane Day
Dept. of Mathematics and Computer Science
San Jose State University
San Jose, CA 95192-0103
day@sjsumcs.sjsu.edu
Thomas Hagedorn
Department of Mathematics
The College of New Jersey
38 Chestnut St.
Princeton, NJ 08542
hagedorn@tcnj.edu
Paul Hurst
Brigham Young University – Hawaii
MSC Division Box 1967
Laie, HI 96762
hurstp@buyh.edu
|
Dan Kalman
Department of Mathematics and Statistics
American University
4400 Massachusetts Avenue, NW.
Washington, DC 20016-8050
kalman@email.cas.american.edu
Andrew Leahy
Dept. of Mathematics
P.O. Box 110
Knox College
Galesburg, IL 61401
aleahy@knox.edu
Michael Penkava
Math Department
University of Wisconsin –Eau Claire
Eau Claire, WI 54702
penkawmr@uwec.edu
John Polking
Department of Mathematics
Rice University
P.O. Box 1892
Houston, TX 77251
polking@rice.edu
Lorenzo Sadun
Department of Mathematics C1200
University of Texas
Austin, TX 78712
sadun@math.utexas.edu
http://www.ma.utexas.edu/users/sadun
|
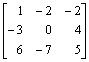 and b =
and b = . Is
. Is 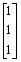 a solution for the system
Ax = b? Explain.
a solution for the system
Ax = b? Explain.
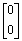 , y1 is a solution to Ax =
, y1 is a solution to Ax =
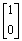 , and
y2 is a solution to Ax =
, and
y2 is a solution to Ax = 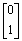 .
.
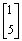 ?
?
 .
.
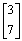 .
.
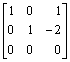 . Find all
solutions to Ax = 0.
. Find all
solutions to Ax = 0.
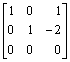 . Find all
solutions to Ax = b.
. Find all
solutions to Ax = b.