The other main focus of the Technology Subgroup was to review the specific uses of technology for teaching linear algebra. After an introductory overview of some commonly used software packages, some members of our group presented more thorough workshops, open to all interested PCMI participants, on the individual programs. Section 3 describes these sessions and presents examples of how to use the various programs as well as references to materials we developed to permit individual experimentation with these programs. A list of the participants of the Technology Subgroup is presented in Section 4.
Among the members of the Technology Subgroup, there was a great diversity as to the size of our institutions, their typical class size, our target audience, and the availability of hardware and software, as well as how much we choose to utilize technology. Six of us usually teach linear algebra classes of between 5 and 20 students, five of us have classes of between 25 and 40 students, one has classes of 80 students and another has a class of 120 students. John Polking described how linear algebra is integrated with differential equations at Rice University; in about one third of a 15 week course they cover just the linear algebra topics essential to understand linear systems of differential equations. For some of us, up to 50% of our linear algebra students are math or math education majors; for others the majority of our students are in science or engineering. It became apparent during our discussions that the manner in which technology can be incorporated into linear algebra instruction depends strongly on all these factors.
Despite these differences, we all agreed on one over-arching principle. Regardless of whether one will be creating new materials or using materials prepared by someone else, one should have a clear educational objective, and consider whether the use of technology will enhance this purpose enough to outweigh the time and effort required to implement it. If there is no compelling advantage to using it, technology should probably be avoided.
While it would certainly be inappropriate to neglect rigorous proofs of such conjectures and theorems, we all know that to create or understand a proof, we use our intuition as a guide at the beginning. Appropriate calculations can aid in building and confirming that intuition. Without technological assistance, it can be much harder to generate sufficient data to draw conclusions, and students may become so distracted by the details of calculations that they miss the general patterns we want them to recognize.
Lessons given in worksheet form, as can be done with Maple and Mathematica for example, are much easier to use and can actually promote mathematical writing by students. If encouraged to do so, students may insert extended prose explanations to accompany their computer calculations. They will also tend to learn, by the instructor's example, to use the formatting capabilities of a worksheet to produce a more professional looking finished product. Besides these benefits, since the necessary computer instructions may be integrated into the lesson text, students may quickly utilize the technology with less difficulty and distraction. Cutting and pasting the given instructions greatly reduces the number of frustrating typographical errors and as a consequence students are able to quickly learn to use the technology. As these worksheets may be submitted electronically, the instructor may even find a more efficient way to grade and maintain permanent records of student work.
Historically, not only the order in which we have presented material, but even the topics we chose to cover have been heavily influenced by the students’ ability to compute. Technology may be used to reshape the curriculum more effectively. For example, we can now introduce more realistic applications of linear algebra early in the course, to generate student interest and motivate what is to come. Students can appreciate the importance of such concepts as inverses or determinants well before they master the computations by hand. They can now easily create accurate and compelling dynamic geometric representations of linear algebra concepts in a way that was impossible before.
Independent of the material itself, technology may be also used to improve the dynamics of student learning. For example, one can create self-directed curricular materials to encourage students to take responsibility for their own learning. Such materials can allow the brightest students to stay fully engaged, by exploring the material at a deeper level, while permitting weaker ones to fully digest the basic material at their own pace. This can reduce frustration and promote success without sacrificing either mathematical content or technical proficiency in computation. In addition, such materials can allow for the small group interactions which foster students’ communication skills.
Also, the results of students' calculations should be discussed. Otherwise students may be left with gaps in their understanding. Facility with a software package may allow them to mask their lack of understanding. As in any teaching situation, it is always critical that we, as instructors, find ways to carefully probe what students really know, as opposed to what they seem to know (cf. the report of the Pedagogy Subgroup). In general, it can be very hard to distinguish between a student's fluency in the use of a particular technology and its associated algorithms, and a true understanding of the mathematics which they are supposedly demonstrating.
Technology can also introduce new and unanticipated types of difficulties. Equipment and software will not always work properly, and there can be administrative hassles. Anyone considering using technology should determine what institutional sources of technical support will be available. It is strongly recommended that a graduate or undergraduate student who has experience with the technology be available in any computer lab setting (Note: This often eventually occurs on its own over time if the same technology is used consistently in a number of courses).
More difficult for many of us is recognizing how this new tool forces our teaching style to change. By giving students more control over the learning environment, we must adapt to having less control and being more flexible. We must be cognizant that they may discover mathematical truths that we did not expect them to find, and not let technology short-circuit the learning process.
Here I present a project using Maple which illustrates the action of a one-parameter family of 2 by 2 matrices on the plane. I find that many of my students (even those who have passed a first course in Linear Algebra) have difficulty understanding basic features of the action of linear transformations. For example, they have no idea what kind of region could represent the image of a cube under a linear transformation in R3, L(X)=AX, or that the volume of the image of the unit cube is given by the determinant of A.
I have never taught a Linear Algebra course with technology, but recently I offered a reading course in Dynamical Systems to a group of three computer science majors. The course repeatedly used several Linear Algebra concepts and I created several projects to illustrate them. In this note I plan to describe one of the projects that the students found particularly helpful. First, I want to point out that as none of the students had any previous knowledge of Maple, I started by preparing an introductory lab assignment where basic Maple commands and computations were introduced. Students could then experiment with and become familiar with the standard syntax of Maple as well as Maple's Help menu. I find it very helpful to dedicate some time to exploring the Help menu and teaching my students how to efficiently use it. Students become familiar with looking for key words and thereby become better equipped to solve their own problems while using the computer algebra. Let me start by considering 2 by 2 matrices of the form Ma=
I found that this project really helped students to visualize what was actually happening. Since the chosen transformations made it possible to perform hand computations, I noticed that at the beginning students were checking Maple's outcomes by actually performing the calculations by hand. I also noticed that as they became more familiar with the computer algebra they felt more secure and more focused on interpreting what they were observing. I believe this is an important aspect in understanding the role of technology. It is an efficient tool which simplifies monotonous calculations and allows students to concentrate on the more important concepts.
Here are two computer assignments that I recently made that were effective and had a delightful and unexpected payoff. Our text12 introduces linear combination and linear independence in Rn quite early, right after systems of equations. After we discussed these new ideas, I asked students to do exercises 42 and 44 in Section 1.6 of the text. At first look these are just a nice application of the definition of independence. This pair of exercises provides a 5x6 integer matrix and asks students to 1) identify a largest independent set of columns, and 2) show that one of the other columns can be obtained as a linear combination of that independent set. The matrix happens to have rank 4.
I decided to discuss this exercise at the following class; my goal was to be sure students could not only solve it but that they recognized that the same linear combinations among columns which are obviously valid for the row-reduced echelon form of a matrix are also valid for the columns of the original matrix.
So at the next class I started MATLAB and the projector, stored the matrix as A, and then typed R = rref(A). They all agreed this was what they had done, and then they had inspected the row-reduced echelon form to identify four pivot columns in A, put those four columns into a matrix B, and calculated rref([B y]) for one of the two nonpivot columns y. They seemed confident about this, but still were interested to learn that everyone had solved the problem the same way. Then I told them they didn't really need to do the second calculation – the solutions to Bx = y were already visible in the row-reduced echelon form of A, for both nonpivot columns y. Apparently no one had noticed that, but they stared at A and R as I covered up columns appropriately, and saw quickly that each nonpivot column of R is a linear combination of the pivot columns on its left; and then saw why that same relationship is valid for the columns of A. I pointed out this would be true for any matrix, for the same reasons. They seemed very satisfied with this discussion. In the past I've done similar discussions using a chalkboard, but the computer demonstration was definitely more vivid and held their keen attention.
I moved on to assign a computer project I have written, "Rank and Linear Independence."4 This project defines rank(A) as the number of pivot columns of A and explores the connection between rank and independence of columns. (In the text, rank is introduced much later, but I like to present it early.) The last question in the project asks students to experiment with random entry matrices of a variety of shapes and make a conjecture about rank(A) and rank(AT). I’ve posed that question early in my classes for years. There are always students who claim that this is a theorem because it’s true in all the examples they have tried, or because the row-reduced echelon form of A has the same number of pivot positions in its rows as in its columns.
It did not occur to me that the class discussion we'd just had revealed a correct proof of the conjecture, so when I graded the projects I was looking as usual for the common errors, and I found some of those. Then I discovered to my delight that one student had both understood what was needed and had nearly proved the theorem: she said the row-reduced echelon form shows that every nonpivot column of A is a linear combination of the pivot columns on its left, so column reduction of A would have to zero out those nonpivot columns, hence rank(AT) cannot be larger than rank(A). She wasn’t sure how to conclude they were equal. At the next class I congratulated her and told the class no student of mine had ever done this before! We discussed what she had seen and when I suggested that she try applying her result to AT, she saw it at once how to complete the argument. (What had happened in earlier semesters when we discussed this project was that everyone agreed that it looked like A and AT always have the same rank; then I would emphasize that examples don't prove this but that we would see a proof eventually.)
So how did computer use make the above work more effective? The obvious answer for the text problem and our discussion of it is that we could focus attention on concepts, not arithmetic. Students could have done the row-reduction by hand, but chances are some would have made arithmetic mistakes and missed much of the point. I could have presented A and its reduced echelon form on a transparency, or written them on the board. But I think many students still would have been somewhat worried about the arithmetic, especially if my numbers were different from theirs. Using MATLAB removed doubt about the arithmetic and allowed us to spend more time on concepts. We could focus confidently on the numbers in A and its row-reduced form and think more deeply about what those told us. (Of course there is no way of knowing whether that gifted student would have had the same insight if we had done only hand calculations.)
Clearly the exploration of rank of random matrices would be miserable by hand but is easy with MATLAB, and it does not take long for every student to conjecture that rank(A) = rank(AT) is true. Finally, as mentioned above, I find that students watch a computer demonstration intently, especially if such demonstrations alternate with other activities.
In Anton's book, Elementary Linear Algebra1, section 9.5 deals with quadratic forms (products of the form xTAx, where A is a symmetric n by n matrix). This is equivalent to taking the inner product of Ax and x. There are a number of problems on page 477 involving the quadratic form. The first problem asks for the maximum and minimum values of the quadratic form with the constraint that the vector x has euclidean norm 1. The main theorem is as follows:
Let A be a symmetric n by n matrix whose eigenvalues in decreasing size order range from l1 to ln. If x is an n by 1 vector whose euclidean norm is one, then:Now, technology can be used to illustrate the meaning of and verify this theorem. First we explore what the values of the inner product are when different vectors of norm one are used. Then we graph these values against their arguments. Note in both cases that they all lie between the eigenvalues of A, which are -1 and 3. These exercises should help the students to understand what the theorem means.
- The inner product of Ax and x is between l1 and ln.
- The inner product of Ax and x is equal to l1 if x is an eigenvector of A corresponding to l1 and the inner product of Ax and x is equal to ln if x is an eigenvector of A corresponding to ln.
To begin, a student should load the linear algebra package, define a matrix
> with(linalg): > A := matrix(2,2,[1, 2,2,1]);eigenvalues(A);
The following short program will then compute a range of values for xTAx, as x ranges around the unit circle:
> for r from 0 to 10 do > t := evalf(2.0*Pi*r/10): > x:=matrix(2,1,[cos(t), sin(t)]): > v[r] := evalm(transpose(x)&*A&*x); > print(t,evalm(v[r])); > od:
We can then define a function f1(t) which represents xTAx:
and then generate a plot of f1(t) as a discrete list of points:> f1 := proc(t,A) > local x; > x := vector([cos(t),sin(t)]); > innerprod(x,A,x); > end;
Alternatively, we can generate a continuous plot:> l := [[ 2*Pi*n/100, f1(2*Pi*n/100,A)] $n=1..100]: > plot(l, x=0..2*Pi, style=point,symbol=circle);
The student can explore what happens when other 2 by 2 matrices are used, including a matrix with complex eigenvalues and a matrix that is not symmetric. Another question that can be explored is "Why does it appear that there are 2 values that give the value of 3 and two that give the value of -1?" You can also require the students to come up with an expression (in terms of sin and cos) of the function.> f2 := proc(t) > local x; > x := vector([cos(t),sin(t)]); > innerprod(x,A,x); > end; > plot(f2(t),t=0..6);
In this example, which is adapted from the laboratory manual Linear Algebra with Maple, we consider how to use technology to explore the notions of linear independence and the span of vectors in Rn. Problems involving these concepts can be solved either by setting up a system of linear equations, which can be solved directly by various software packages, or by converting the problem directly into one which involves Gauss-Jordan elimination of a certain matrix. The former approach has a more direct connection to the conceptual framework, while the latter approach is easier to implement by hand, but the technology makes both approaches equally easy to calculate.
Problem 1: Let S be the subspace of R4 spanned by the vectors u1:=(1,2,3,4), u2:=(4,2,1,5), and u3:=(3,5,1,7). Determine if the vectors v:=(8,9,5,16) and w:=(7,2,1,3) are in S.
This problem is solved by considering the expression v:= x1u1 + x2u2+x3u3 as a system of 4 equations in 3 unknowns. In order to solve this problem using MapleV, the elements of R4 are entered as vectors. Thus, the equation for v above is really a vector equation, rather than a system of equations. The student will need to learn how to convert the vector expression into a system of linear equations, and the textbook gives a Maple procedure which will take care of this conversion. Solving this system directly yields the solution {x1=1, x2=1,x3=1}. A similar approach with w will yield no solution. An alternative method is to consider the augmented matrix A:=[u1 u2 u3 v w], and find its reduced row echelon form. The latter method also allows one to express v as a linear combination of the vectors u1, u2, and u3, by looking at the coefficients appearing in the fourth column of the reduced row echelon form.
The textbook also consider problems such as finding a vector that is not in a subspace spanned by a set of vectors in Rn and determining whether a set of vectors is a basis of Rn. Several different solutions are worked out for these problems. There are also problems involving vector spaces of matrices, including one in which the intersection of 2 subspaces of M2,2 is described, as well as vector spaces of polynomials,
All of these problems have the nice feature that they focus the student to focus on the concepts involved. By first having them pose the question in mathematical terms, as seen above by posing the equation first as a vector equation, and then using the technology to convert this formulation into a form in which it can be solved, students are able to distinguish the different ideas involved in the problem. Also, by having the students use multiple approaches to the same problem, these ideas may become clearer to the student. When students solve a problem by merely applying a simple algorithm, such as determining whether a set of vectors is linearly dependent by forming a matrix with these vectors as columns and reducing it to echelon form, there is a great danger that they will substitute memorization of a routine for understanding of the concept. But through the use of technology as it is demonstrated in the exercises involving vector spaces and their subspaces in this manual, students may develop a better understanding of the underlying concepts. In addition, more difficult exercises such as the one involving the intersection of subspaces of the vector space of 2 x 2 matrices become possible for the student to carry out successfully.
This exercise on Matrix Population Models should actually be considered a project. It is too long and difficult to be a simple exercise. It demonstrates an actual use of matrices and their eigenvalus and eigenvectors. It would be very hard to complete the project without using a computer, since it requires the computation of eigenvalues and eigenvectors for many matrices which are four by four and five by five. Furthermore, the entries are not small rational numbers, and in the more interesting second section the entries themselves need to be computed. The project is best done by doing some elementary programming. It can be done without that, but it is difficult, especially in the second section. The needed programming can easily be done in MATLAB, and probably is not difficult in other mathematical programs. The project encourages the student to experiment with the model to see the effects of different ecological strategies. It should be emphasized that the model in the second section was actually used by the federal government and by some state governments to decide on their ecological strategies.
In this exercise we will illustrate the application of eigenvalues and eigenvectors to the analysis of models of population growth. In the final part we will employ actual data about the life cycles of loggerhead sea turtles to make predictions regarding their survival. We will also use the model to analyze the effectiveness of several strategies for improving the chance that the species will survive.
There are two factors involved — birth and death — that
change the populations from year to year. We will assume that each
age group has its own death rate dk, and define the
survival rate for this group by sk = 1 -
dk. Thus
![]() is the number of newborns in
cycle n + 1 and will be the sum of the births to all age
groups. The group of age k - 1 must first survive to age
k and then reproduce, so the number of births from this group
will be
is the number of newborns in
cycle n + 1 and will be the sum of the births to all age
groups. The group of age k - 1 must first survive to age
k and then reproduce, so the number of births from this group
will be ![]() . The total number
of newborns in cycle n + 1 will therefore be
. The total number
of newborns in cycle n + 1 will therefore be
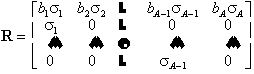 . (3)
. (3)
We can analyze the evolution of the population by using information about the eigenvalues and eigenvectors of the projection matrix. For now, let's assume that R has A distinct eigenvalues, r1, ..., rA. For each of the eigenvalues, rk, we can find an associated nonzero eigenvector vk. Under the assumption that the eigenvalues are distinct, it follows that this set of eigenvectors form a basis. Once again, this means that the initial population vector p(0) can be written as a linear combination of the eigenvectors, i.e., there are constants ck such that
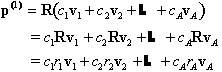
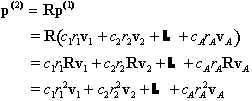
Before proceeding further, we will make another hypothesis. We will assume that one of the eigenvalues is real, positive, and larger than the absolute values of each of the others. We will assume that we have labeled the eigenvalues so that this one large eigenvalue is r1. r1is called the dominant eigenvalue. (MATLAB may not choose to place the dominant eigenvalue first when calculating eigenvalues.)
Under this assumption, it is easy to analyze what happens to p(n) as n goes to infinity. Dividing (7) by
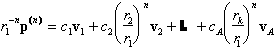
It follows that, in the limit of a large number of reproductive cycles, the components of the population vectors p(n) have ratios which are independent of n, i.e.,
As noted above, eigenvectors can be ``normalized'' in a variety of ways; in other words, each eigenvector can be multiplied by an arbitrary constant and still be an eigenvector. In the population context, it is usual to normalize a stable age distribution vector by requiring that the sum of the entries is 1. Then each entry gives the fraction of the total population which is in that age group.
The size of the dominant eigenvalue is also important. If
As before, we assume that the species undergoes a cycle of reproduction and change. During this cycle the individuals in the kth stage may stay in the kth stage or be transformed into one of the other stages. The probability that an individual in the kth stage will go into a new stage, i, is denoted by rik. Thus if p(0) is the population vector in the nthcycle, the number of individuals in the kth stage at the (n + 1)st cycle is
p(n + 1) = Rp(n),
p(n) = Rnp(0) (10)
Since everything in the previous section depended on (5), all of the results of that section apply here as well. In particular this is true of the analysis of the asymptotic behavior of the population vector, and the importance of a dominant eigenvalue and its associated eigenvector.
We will now apply these concepts and methods to the population of loggerhead sea turtles. Marine turtles, as typified by the loggerheads are long-lived and mobile3. Only the adult nesting females, eggs and hatchlings, and stranded, dying turtles are ever seen on beaches. Furthermore, no method has been devised to obtain accurate age information about sea turtles. These reasons pretty much preclude obtaining information of the detail that would be required to use an age-based model of the type described in the previous section. For these reasons, it was decided to use a stage-based model, by dividing the population into five stages. The stages, stage durations, survivorships, and birth rates are shown in Table 1. The data in Table 1 are the result of long observation of loggerhead sea turtles6.
Table 1. Five-stage life history parameters for loggerhead sea turtles.
|
Stage |
Description |
Stage duration (yr.) |
Annual survivorship ( s) |
Annual birth rate |
|
1 2 3 4 5 |
Eggs/hatchlings Small juveniles Large juveniles Subadults Adults |
1 7 8 6 >32 |
0.6747 0.7500 0.6758 0.7425 0.8091 |
0.0 0.0 0.0 0.0 76.5 |
An individual in one of the stages can survive and stay in the same stage or it can survive and move on to the next stage. Consequently the population projection matrix has the form
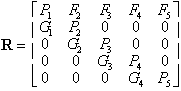 (11)
(11)
Calculating the probabilities in the population projection matrix for the stages that have a duration longer than one year is a little complicated, so we will go through it step by step. If the duration is d years in stage k, then there are individuals in that stage who have been there for 1, 2, …, d years. The probability of any individual surviving to the next year is the survival rate, s k, in Table 1. The probability of surviving y years is
Only the individuals with the highest age in a stage move onto the next stage. Hence, the relative number of them is
From this we see that the probability of surviving and going on to the next stage is the product
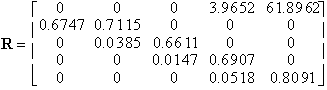
It has been estimated that as much as 70 – 80% of the deaths of turtles in stages 3, 4, and 5 are due to turtles being caught in the nets of shrimp trawlers. There is a device, called the Turtle Excluder Device, or TED, which is effective in allowing turtles to escape from shrimp nets. TEDs were required of shrimp fishermen in the southeast US from 1990 to 1992, but no longer. Shrimp fishermen object to the use of TEDs on the grounds that they are expensive and they reduce the size of their catch. In some states they have become a serious political problem.
The following is an expanded version of an exercise I gave my students to explore what the effect is of left-multiplication or right-multiplication by a given matrix. The idea is to see that left-multiplication is taking linear combinations of rows, and that right-multiplication is taking linear combinations of columns, and in particular that elementary row operations correspond to left-multiplication by elementary matrices.
This exercise is platform-independent, and is intended as part of a weekly problem set. It can therefore be used even in large lecture courses that have no computer lab, as long as the students have access to technology somewhere. If you are teaching a course with a regular computer lab, you might consider expanding this exercise into a full-fledged workbook utilizing your local software.
The primary value of this exercise is in encouraging experimentation. By playing around with the product of given simple matrices and student-generated random matrices, students get a feel for the action of elementary matrices, can form conjectures, and can test these conjectures. This easy experimentation lets students get a grip on abstract concepts that would otherwise be out of reach. These values are somewhat limited by the problem-set form of the exercise, which tends to lead students by the nose. A workbook version of these exercises could leave room for free exploration in the early steps and then provide explanations (and opportunities to verify statements) later in the workbook.
Let A be any old 5 by 5 matrix. Just type in arbitrary entries, or use a random matrix generator. Now let P, E, T, and D be as follows:
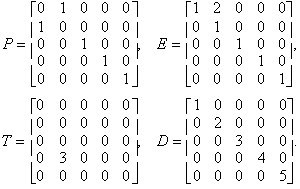
Another good example of a good technology-assisted assignment comes from the ATLAST project’s Computer Exercises for Linear Algebra13. This is a collection of different short projects, each of which may be carried out as a classroom demonstration, lab project, or homework exercise, either individually or in groups. One nice example (p. 146 – 7) focused on the significance of an eigenvector. Using a mix of compelling computer graphics, numerical calculations, and traditional proof techniques, the author helps them to discover that powers of a matrix applied to a vector generally converge to lie in a 1-dimensional subspace corresponding to the eigenvector corresponding to the largest magnitude eigenvalue. At the outset, students were assumed to know what is meant by a unit vector, how to visualize two-dimensional column vectors in the plane, the definition of eigenvector v with associated eigenvalue l of a matrix A, Av = lv, and the concept of "diagonalizeability". By the end of the project, students have a fuller understanding of the algebraic and geometric significance of eigenvectors and eigenvalues, experience writing simple proofs based on this definition, and a basic understanding of the numerical algorithm, called the "Power Method" for computing eigenvectors of symmetric matrices.
The author has the students begin with an asymmetric matrix with rows that add to 1 and observes that this must have an eigenvector of w = [1 1]T with associated eigenvalue 1. They then use MATLAB’s eig command both to verify this observation and display the remaining eigenvector, v, with associated eigenvalue = .78. Students then take a unit vector u in the plane (that was chosen not to be an eigenvector) and use the author’s powplot command to see a picture of a sequence of vectors Aiu plotted in the plane (for i = 1, … , 25). If fact, the picture also shows the successive images of the entire unit circle under Ai. At this point, the instructor should be careful to explain what the pictures represent, since students may misinterpret them in unexpected ways.
Using the powplot command, students can see the convergence to a multiple of the dominant eigenvector. By repeating this experiment many times, students observe that this almost always seems to occur, although some resulting vectors are larger than others. They may or may not yet notice that they can achieve a 0 result.
However, the author then directs students to use powplot applied to the other eigenvector v. He first has them observe that Aiv converges to 0. He then has them prove this fact. He then encourages students to explore the eigensystems of other 2x2 matrices to observe the connection between the dominant eigenvector (which he defines) of a matrix and it associated powers. After students have an experimental basis for the theorem, they are require to prove that, for a diagonalizable matrix A, Aiu converges to the dominant eigenspace. They conclude the lab by learning to carry out these calculations numerically using the "Power Method."
This lab has a number of good features. It uses experimentation to lead students to important mathematical concepts and proofs. Moreover, it helps to build students’ intuition through direct experience with numerical calculations (of eigensystems and iterated powers) and computer graphics, without requiring students to key in more than a few simple commands. This all would have been impossible without the use of technology.
Consider the benefit of being able to provide the powplot command as a pre-defined MATLAB program (called an M-file), instead of requiring the students to type in all the corresponding program instructions themselves. Without the command, students would have spent the overwhelming amount of time typing and may have been less likely to make the quantity or quality of observations that they could otherwise. In this example, we can see the benefit of a programmable environment (such as MATLAB, Maple, or Mathematica), where students may load a program without typing it explicitly. Moreover, since this program, and many others, are freely available for download over the Internet, instructors do not need to become programmers in order to use a wide variety of demonstration software.
Finally, although this entire lab was designed to be done after a good deal of class discussion of eigensystems, parts of the lab could be used much earlier to motivate the definition of an eigenvector and eigenvalue. By giving students a concrete motivation for these important definitions, they will be more likely to remember them. Overall, the class will be well-rewarded for the time spent on this lab project.
The technology tools we explored were the ones available at this institute. These do not exhaust what is available, and we have no wish to endorse any specific ones. Indeed, it is clear from our discussions that the question of which tool a teacher chooses to use in linear algebra will depend strongly on taste and local factors at one's school such as the availability of software and what is used in other courses. Regardless of what software or calculator is chosen, we recommend it be able to automate routine tasks such as matrix multiplication, Gauss-Jordan elimination, calculation of eigenvalues, and plotting in R2 and R3.
During the 1.5 hr. demonstration, all of the presenters were directed to use their technology to solve the following two exercises:
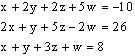
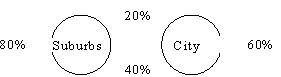
This was intended to highlight the similarities and differences between the various technologies. The presenters also provided some combination of printed and/or computer documents to instruct the participants on how to use the technology themselves to solve such basic linear algebra problems.
What follows are some materials submitted by each presenter regarding the technology that they demonstrated. Some have chosen to include the material from their presentation, while others have provided a more general discussion of the strengths and weaknesses of their technology, or a combination of the two.
About 2 years ago, when I first became a professor at the University of Wisconsin, Eau Claire (UWEC), I began looking into computer algebra systems for the math department. We chose to purchase a site license for Maple V partially because the company made a special effort to make it affordable for of. At the ti software . Regardless of whatanalculus d we assume that each yerive and ISETL. The similarity of the ISETL programming language to Maple made the transition fairly smooth for us.
In choosing a software platform, price can be an important factor, but it is also important to consider whether the software can be used for a variety of applications. Our department has been able to use Maple software as an effective teaching tool in our technology oriented calculus classes. In addition, some of the faculty have used this software to enrich our linear algebra and abstract algebra courses. This summer I attended a workshop for the purpose of designing a mathematics course for a new Computational Science minor at UWEC that will feature the use of Maple for a variety of computational applications. I plan to use Maple as a technological aid in a differential equations course that I will be teaching this fall.
When choosing an appropriate technology to augment a linear algebra course, it is also important to consider the software the students will have been exposed to in their calculus course, as well as the type of software that students will likely use in their majors. At my university, Maple meets this requirement of being used in calculus, linear algebra, and in other science classes. Some members of the mathematics faculty of UWEC are working to further integrate the use of this technology into the curriculum. Their hope is that students will develop computer skills in their early courses whichssions that thin the upper division curriculum. In order to integrate technology as part of the classroom environment, the department is in the process of constructing a combined laboratory classroom so that the computer will be able to be used, when appropriate, during class.
Let me now discuss some features of the Maple program. Maple has a feature that allows the instructor to give out the laboratory assignments on a computerized worksheet. The instructor can embed whatever software hints and special functions he/she wishes within the assignment, so there is no need to download special packages to do the computer assignment. At my university, students submit their worksheets electronically by placing them in a directory accessed by the professor. The professor can then grade the assignments and add comments electronically, and students can then use these comments to improve their work and resubmit it. The worksheet feature greatly eases this type of interaction. An additional feature of Maple is that students can write Maple procedures, which are essentially mathematical functions. Writing these procedures is similar to the way a mathematician defines a function. Initially, students have some problems with Maple because they fail to distinguish between expressions and functions. But as they resolve these problems, they are better able to understand what a mathematical function is.
Maple has a built-in linear algebra package with all the standard matrix functions. In addition, the simple structure of the programming language makes it relatively easy for students to construct their own special functions. One of my students, in a special project for the linear algebra class, studied exponentiation of Jordan block matrices in order to understand how the general exponential function of a matrix can be calculated. The student wrote a simple Maple procedure to create a Jordan block of an arbitrary size (there already exists a pre-defined Maple procedure which does this). The ease with which the procedures can be constructed can be an asset in the student’s understanding of mathematics. Also, Maple does exact algebra, instead of floating point approximations, and is symbolic. Hence, matrix calculations can be done with variables as coefficients and this makes it easy to write worksheets illustrating such concepts as linear dependence and span.
Let me note that there are some features of the Maple program which can be annoying. For example, Maple does not print the contents of the matrix if you simply type the name of the matrix, so to print the matrix A, you must type evalm(A). This can be confusing to the students at first. Also, the syntax of the linear algebra commands is not always consistent, and the help function, while extensive and detailed, can sometimes be confusing.
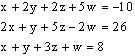
Solve[{x+2y+2z+5w == -10, 2x+y+5z-2w == 26, x+y+3z+w == 8}]and then hit Shift-Return to tell Mathematica to evaluate this expression. This has the advantage that the command strongly resembles the language of the original question. The disadvantage is that the phrasing of the result may seem unusual.
A={{1,2,2,5,-10},{2,1,5,-2,26},{1,1,3,1,8}};and again hit Shift-Return. Notice how Mathematica represents a row as a curly-bracketed list, and a matrix as a list of lists. This has the advantage of using the language of matrix algebra, but some may find the notation disturbing.
RowReduce[A]
Start MATLAB. You will see the Command screen and the prompt >>. After this prompt you can type any valid MATLAB command and then press [Enter] to execute the command. In what follows, MATLAB commands will be written in boldface.
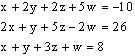
A = [1 2 2 5; 2 1 5 –2; 1 1 3 1]
b = [-10; 26; 8]
rref([A b])
A = [1 2 2 5; 2 1 5 –2; 1 1 3 1], b = [-10; 26; 8], rref([A b])or by creating the augmented matrix to start with, and reducing that:
M = [1 2 2 5 -10; 2 1 5 –2 26; 1 1 3 1 8], rref(M)
p = p0; P = [p0]; for i = 1:12, p = A*p; P = [P p]; end(i.e., store p0 and 12 iterates in P, using ";" to suppress printing) P (see P)
x = 2000:2013; plot(x, P)(Store x-values in x and plot each row of P against x)
axis([2000 2015 5 12] , shf(Set limits for x and y axes and type shf to show figure)
rref([A – eye(2)]
and writing the general solution. Another way is to calculate all eigenvalues and eigenvectors of A and select an eigenvector corresponding to 1. To do that, type [V D] = eig(A). You will see
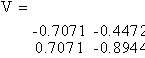
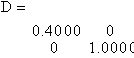
The diagonal entries of D are the eigenvalues of A, and column i of V is an eigenvector corresponding to D(i,i). So column 2 of V is an eigenvector corresponding to the eigenvalue 1. To store that as a separate vector, type p = V(:, 2) .
The algorithm in eig always produces columns in V which have Euclidean norm 1, but it is easy to scale these as you wish. For example, to get an eigenvector corresponding to the eigenvalue 1 which has sum 9, type p = (9/sum(p))*p.
The following are the steps one uses to input a matrix into the TI-86. In many cases, these steps are listed by the keys on the calculator that one needs to press.
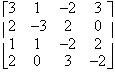 For the determinant:
For the determinant:
The following are the steps one uses to input a matrix into the TI-92. In many cases, these steps are listed by the keys on the calculator that one needs to press.
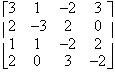
|
Daniel Goroff Department of Mathematics Harvard University Science Center 325 Cambridge, MA 02138-2901 goroff@abel.math.harvard.edu Robert Bolger Fairfield University North Benson Road Fairfield, CT 06430 Fernanda Botelho University of Memphis/Institute for Mathematics 514 Vincent Hall 206 Church St. SE Minneapolis, MN 55455 botelho@irna.umn.edu Harold Davenport Department of CS, Mathematics and Statistics Mesa State College Grand Junction, CO 81502 davenpor@mesa5.mesa.colorado.edu Jane Day Dept. of Mathematics and Computer Science San Jose State University San Jose, CA 95192-0103 day@sjsumcs.sjsu.edu Clifton Ealy Department of Math and Statistics Western Michigan University Kalamazoo, MI 49008-5521 ealy@math-stat.wmich.edu Thomas Hagedorn Department of Mathematics The College of New Jersey 38 Chestnut St. Princeton, NJ 08542 hagedorn@tcnj.edu Paul Hurst Brigham Young University – Hawaii MSC Division Box 1967 Laie, HI 96762 hurstp@buyh.edu
|
Dan Kalman
Department of Mathematics and Statistics
American University
4400 Massachusetts Avenue, NW.
Washington, DC 20016-8050
kalman@email.cas.american.edu
Andrew Leahy Dept. of Mathematics P.O. Box 110 Knox College Galesburg, IL 61401 aleahy@knox.edu Michael Penkava Math Department University of Wisconsin –Eau Claire Eau Claire, WI 54702 penkawmr@uwec.edu John Polking Department of Mathematics Rice University P.O. Box 1892 Houston, TX 77251 polking@rice.edu
Jung Rno University of Cincinnati – RWC 6462 Mayflower Avenue Cincinnati, Ohio 45237-4402 rnojs@ucrwcu.rwc.uc.edu Lorenzo Sadun Department of Mathematics C1200 University of Texas Austin, TX 78712 sadun@math.utexas.edu http://www.ma.utexas.edu/users/sadun Jeanne Wald Department of Mathematics Michigan State University E. Lansing, MI 48824 wald@math.msu.edu John Wicks North Park University 3225 W. Foster Ave. Chicago, IL 60625 jwicks@northpark.edu Wiley Williams Mathematics Department University of Louisville Louisville, KY 40292 wcubed@louisville.edu
|